统计相似字符串对的数目

给你一个下标从 0 开始的字符串数组 words 。

如果两个字符串由相同的字符组成，则认为这两个字符串 相似 。

• 例如，"abca" 和 "cba" 相似，因为它们都由字符 'a'、'b'、'c' 组成。
• 然而，"abacba" 和 "bcfd" 不相似，因为它们不是相同字符组成的。

请你找出满足字符串 words[i] 和 words[j] 相似的下标对 (i, j) ，并返回下标对的数目，其中 0 <= i < j <= word.length - 1 。

class Solution {
public:
    int similarPairs(vector<string>& words) {
        map<set<char>,int> m;
        int ans=0;
        for(auto& str: words){
            set<char>s (str.begin(),str.end());
            ans+=m[s];
            m[s]++;
        }
        return ans;
    }
};

使用质因数之和替换后可以取到的最小值

给你一个正整数 n 。

请你将 n 的值替换为 n 的 质因数 之和，重复这一过程。

• 注意，如果 n 能够被某个质因数多次整除，则在求和时，应当包含这个质因数同样次数。

返回 n 可以取到的最小值。

class Solution {
public:
    int calc(int x){
        int ans=0;
        for(int i =2; i<=x/i;i++){
            while(x%i==0){
                ans+=i;
                x/=i;
            }
        }
        if(x>1) ans+=x;
        return ans;
    }
    int smallestValue(int n) {
        int a=calc(n);
        while(a<n){
            n=a;
            a=calc(a);
        }
        return n;
    }
};

添加边使所有节点度数都为偶数

给你一个有 n 个节点的 无向 图，节点编号为 1 到 n 。再给你整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条边。图不一定连通。

你可以给图中添加 至多 两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回 true ，否则返回 false 。

点的度数是连接一个点的边的数目。

示例 1：

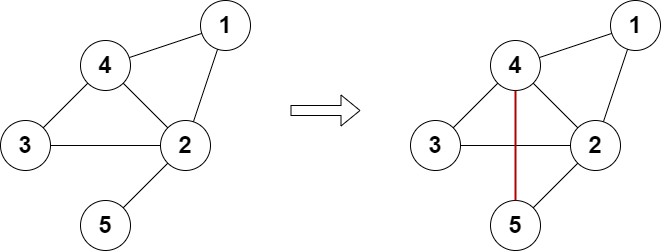
输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

class Solution {
public:
    int d[100010];
    set<long long> m;
    long long calc(int a,int b){
        if(a<b) swap(a,b);
        return 1ll*a*100000+b;
    }
    bool isPossible(int n, vector<vector<int>>& edges) {
        for(auto & e : edges){
            m.insert(calc(e[0],e[1]));
            d[e[0]]++;
            d[e[1]]++;
        }
        vector<int> need;
        for(int i=1;i<=n;i++)
            if(d[i]%2==1)
                need.push_back(i);
        if(need.size()==0) return true;
        if(need.size()==2)
            for(int i = 1 ;i<=n;i++)
                if(!m.count(calc(i,need[0]))&&!m.count(calc(i,need[1])))
                    return true;
        if(need.size()==4)
            do{
                if(!m.count(calc(need[0],need[1]))&!m.count(calc(need[2],need[3]))) return true;
            }while(next_permutation(need.begin(),need.end()));
        return false;
    }
};

查询树中环的长度

给你一个整数 n ，表示你有一棵含有 2n - 1 个节点的 完全二叉树 。根节点的编号是 1 ，树中编号在[1, 2n - 1 - 1] 之间，编号为 val 的节点都有两个子节点，满足：

• 左子节点的编号为 2 * val
• 右子节点的编号为 2 * val + 1

给你一个长度为 m 的查询数组 queries ，它是一个二维整数数组，其中 queries[i] = [ai, bi] 。对于每个查询，求出以下问题的解：

1. 在节点编号为 ai 和 bi 之间添加一条边。
2. 求出图中环的长度。
3. 删除节点编号为 ai 和 bi 之间新添加的边。

注意：

• 环 是开始和结束于同一节点的一条路径，路径中每条边都只会被访问一次。
• 环的长度是环中边的数目。
• 在树中添加额外的边后，两个点之间可能会有多条边。

请你返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 个查询的结果。

示例 1：

输入：n = 3, queries = [[5,3],[4,7],[2,3]]
输出：[4,5,3]
解释：上图是一棵有 23 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后，环为 [5,2,1,3] ，所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后，环为 [4,2,1,3,7] ，所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后，环为 [2,1,3] ，所以第三个查询的结果是 3 。删掉添加的边。

class Solution {
public:
    vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {
        vector<int> ans;
        for(auto& q : queries){
            int cnt=1;
            int x= q[0],y= q[1];
            while(x!=y){
                if(x>y){
                    x/=2;
                }else{
                    y/=2;
                }
                cnt++;
            }
            ans.push_back(cnt);
        }
        return ans;
    }
};