给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个 独立 的查询，其中第 i 个查询你需要执行以下操作：

• 从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

• 查询之间是独立的，所以在每个查询执行后，树会回到其 初始 状态。
• 树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

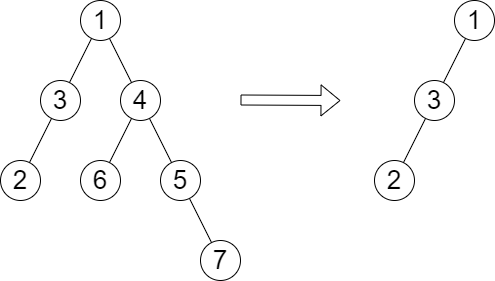
输入：root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出：[2]
解释：上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2（路径为 1 -> 3 -> 2）。

很重要的一个要点要发现，当我移除一个点及其包含的子树后，这个点向上的高度是不会变化的，向下的高度会变化。而向下高度的变化，会由同一层其他的节点的高度决定，即我如果移除了6，应该看2和5哪个点的下面由更多层，从而确定树的高度

因此，任务如下：

首先确定每个节点向上有多少层，向下有多少层，可以通过一次DFS来实现

然后统计同一层有哪些节点（由于val不重复，所以可以通过map存就好了）

在每次查询中，移除一个节点后找同一层的最大值，从而确定答案。

class Solution {
public:
    vector<pair<int, int>> mdep[100001];
    pair<int, int> depth[100001];
    int maxdepth;
    int dfs(TreeNode *a, int d) {
        if (a == NULL) {
            maxdepth=max(maxdepth,d-1); 
            return 0;
        }
        int ans = max(dfs(a->left, d + 1) + 1, dfs(a->right, d + 1) + 1);
        depth[a->val] = {ans,d};
        mdep[d].push_back({-ans,a->val});
        return ans;
    }

    vector<int> treeQueries(TreeNode *root, vector<int> &queries) {
        maxdepth=0;
        dfs(root, 0);
        vector<int> ans;
        for(int i = 0; i < maxdepth; i++)sort(mdep[i].begin(), mdep[i].end());
        for(auto &x: queries) {
            ans.push_back(depth[x].second - 1);
            for(auto &c : mdep[depth[x].second])
                if(c.second != x){
                    ans.back()-=c.first;
                    break;
                }
        }
        return ans;
    }
};