给你一个 n 个节点的带权无向图，节点编号为 0 到 n - 1 。

给你一个整数 n 和一个数组 edges ，其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。

在图中，一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点，且图中存在连接旅途中相邻节点的边。注意，一趟旅途可能访问同一条边或者同一个节点多次。

如果旅途开始于节点 u ，结束于节点 v ，我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说，如果经过的边对应的边权为 w0, w1, w2, ..., wk ，那么代价为w0 & w1 & w2 & ... & wk ，其中 & 表示按位与 AND 操作。

给你一个二维数组 query ，其中 query[i] = [si, ti] 。对于每一个查询，你需要找出从节点开始 si ，在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途，答案为 -1 。

返回数组 answer ，其中 answer[i] 表示对于查询 i 的 最小 旅途代价。

示例 1：

输入：n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

输出：[1,-1]

解释：

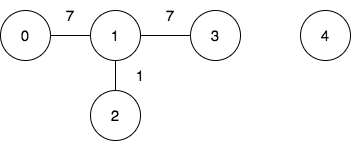
第一个查询想要得到代价为 1 的旅途，我们依次访问：0->1（边权为 7 ）1->2 （边权为 1 ）2->1（边权为 1 ）1->3 （边权为 7 ）。

第二个查询中，无法从节点 3 到节点 4 ，所以答案为 -1 。

示例 2：

输入：n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]

输出：[0]

解释：

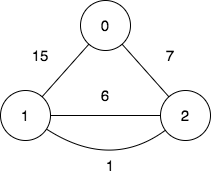
第一个查询想要得到代价为 0 的旅途，我们依次访问：1->2（边权为 1 ），2->1（边权 为 6 ），1->2（边权为 1 ）

一个重要的性质， AND运算不会变大。因此最小的代价可以考虑为把所有能走的路径都走一遍，也就是得到了最小值。

因此任务如下：

把所有的可联通的子图的权值和构建出来，如果这走的是这两个点，则答案为这个联通分量所有的权重的AND运算。否则为-1

因此只考虑分量不考虑路线的方案，采用并查集进行merge合并。

const int MAXN = 1e5 + 10;
int f[MAXN];
int t[MAXN];
class Solution {
public:
    vector<int> minimumCost(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {
        iota(f, f + n, 0);
        memset(t, INT_MAX, sizeof t);
        vector<int> ans;
        function<int(int)> find = [&](int x){
            return f[x] == x ? x : f[x] = find(f[x]);
        };
        for(vector<int> & e: edges){
            int u = find(e[0]), v = find(e[1]), w = e[2];
            if(u == v) t[u] &= w;
            else t[min(u, v)] &= t[max(u,v)] & w, f[max(u, v)] = min(u, v);
        }
        for(vector<int> & q : queries){
            int s = find(q[0]), e = find(q[1]);
            if(q[0] == q[1]) ans.push_back(0);
            else if(s == e) ans.push_back(t[s]);
            else ans.push_back(-1);
        }
        return ans;
    }
};