2508. 添加边使所有节点度数都为偶数

给你一个有 n 个节点的 无向 图，节点编号为 1 到 n 。再给你整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条边。图不一定连通。

你可以给图中添加 至多 两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回 true ，否则返回 false 。

点的度数是连接一个点的边的数目。

示例 1：

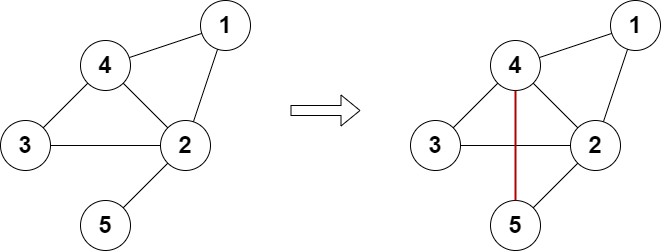
输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

示例 2：

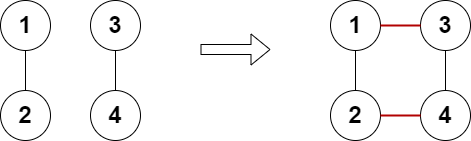
输入：n = 4, edges = [[1,2],[3,4]]
输出：true
解释：上图展示了添加两条边的合法方案。

示例 3：

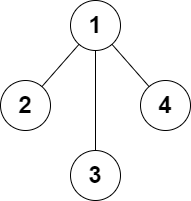
输入：n = 4, edges = [[1,2],[1,3],[1,4]]
输出：false
解释：无法添加至多 2 条边得到一个符合要求的图。

提示：

• 3 <= n <= 105
• 2 <= edges.length <= 105
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• 图中不会有重边

核心问题，统计完所有点的度后，可以考虑一下有多少个度是奇数的，

因为最多可以增加两条边，所以度最多增加4，首先考虑需要处理的点数大于4则无解

然后考虑0-4的所有情况， 0 肯定可以了

1 的话呢，无论如何添加这条边，都会让其和另外一个点的度数同时 + 1 ，则出现一个已知为偶数的点变成奇数，同理3也无解

则考虑2和4

在2的情况下，有两种可能，首先是2和4本身妹有边，则直接链接，完成任务

但是还存在一个情况2和4本身是有变的，则此时可以找一个点x构造出x->1 ,x->2的两个边从而实现x的点的度数增了2，仍然为偶数，需要改的边各增加了1，此时枚举判断。

度数为4的时候，则要考虑缺的4个边是不是存在一个两两组合的方式使得这个组合方案可以各增加一度

class Solution {
public:
    set<int> e[100010];

    bool isPossible(int n, vector<vector<int>> &edges) {
        for (auto &ed: edges) {
            e[ed[0]].insert(ed[1]);
            e[ed[1]].insert(ed[0]);
        }
        vector<int> need;
        for (int i = 1; i <= n; i++) {
            if (e[i].size() % 2 == 1) {
                need.push_back(i);
            }
        }
        if (need.size() == 0) return true;
        if (need.size() %2 == 1) return false;
        if (need.size() == 2) {
            if (!e[need[0]].count(need[1]))
                return true;
            for (int i = 1; i <= n; i++) {
                if (!e[i].count(need[0]) && !e[i].count(need[1])) {
                    return true;
                }
            }
            return false;
        }
        if (need.size() == 4) {
            do {
                if (!e[need[0]].count(need[1]) && !e[need[2]].count(need[3]))
                    return true;
            } while (next_permutation(need.begin(), need.end()));
            return false;
        } 
        return false;
    }
};

---