本周周赛很简单....就是吧这个T4头铁了,觉得差3个点,特判就过了。就听取WA声一片
今天整体还行,预测上40。
阿三如果去掉,应该能上Knight拿牌子了
T1:移除字母异位词后的结果数组
给你一个下标从 0 开始的字符串 words ,其中 words[i] 由小写英文字符组成。
在一步操作中,需要选出任一下标 i ,从 words 中 删除 words[i] 。其中下标 i 需要同时满足下述两个条件:
0 < i < words.length
words[i - 1] 和 words[i] 是 字母异位词 。
只要可以选出满足条件的下标,就一直执行这个操作。
在执行所有操作后,返回 words 。可以证明,按任意顺序为每步操作选择下标都会得到相同的结果。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。例如,"dacb" 是 "abdc" 的一个字母异位词。
输入:words = ["abba","baba","bbaa","cd","cd"]
输出:["abba","cd"]
解释:
获取结果数组的方法之一是执行下述步骤:
- 由于 words[2] = "bbaa" 和 words[1] = "baba" 是字母异位词,选择下标 2 并删除 words[2] 。
现在 words = ["abba","baba","cd","cd"] 。
- 由于 words[1] = "baba" 和 words[0] = "abba" 是字母异位词,选择下标 1 并删除 words[1] 。
现在 words = ["abba","cd","cd"] 。
- 由于 words[2] = "cd" 和 words[1] = "cd" 是字母异位词,选择下标 2 并删除 words[2] 。
现在 words = ["abba","cd"] 。
无法再执行任何操作,所以 ["abba","cd"] 是最终答案。 1 <= words.length <= 100
1 <= words[i].length <= 10
words[i] 由小写英文字母组成唔,这个题周赛隔几周就出一次呀。思路就是用栈模拟,具体操作就是:
1.首元素入栈。
2.即将入栈元素和栈顶元素是否满足字母异位词关系,如果是,就不操作。否则就入栈。
最终就出结果了,因为vector有pop_back()和push_back()操作,所以直接用vector当栈来用就可以直接出结果了
class Solution {
public:
vector<string> removeAnagrams(vector<string>& words) {
int n = words.size();
vector<string> ans;
ans.push_back(words[0]);
for(int i = 1;i<n;i++){
string a=words[i];
string b=ans.back();
sort(a.begin(),a.end());
sort(b.begin(),b.end());
if(a!=b){
ans.push_back(words[i]);
}
}
return ans;
}
};T2:不含特殊楼层的最大连续楼层数
Alice 管理着一家公司,并租用大楼的部分楼层作为办公空间。Alice 决定将一些楼层作为 特殊楼层 ,仅用于放松。
给你两个整数 bottom 和 top ,表示 Alice 租用了从 bottom 到 top(含 bottom 和 top 在内)的所有楼层。另给你一个整数数组 special ,其中 special[i] 表示 Alice 指定用于放松的特殊楼层。
返回不含特殊楼层的 最大 连续楼层数。
输入:bottom = 2, top = 9, special = [4,6]
输出:3
解释:下面列出的是不含特殊楼层的连续楼层范围:
- (2, 3) ,楼层数为 2 。
- (5, 5) ,楼层数为 1 。
- (7, 9) ,楼层数为 3 。
因此,返回最大连续楼层数 3 。1 <= special.length <= 105
1 <= bottom <= special[i] <= top <= 109
special 中的所有值 互不相同这个也比较简单吧,就是如果是在首尾的话,就是最小的special元素减去bottom,如果是队尾的话就是top-$$special_{max}$$
如果是中间就是两个元素的差值-1
然后就特判一下首尾,然后循环special
class Solution {
public:
int maxConsecutive(int bottom, int top, vector<int>& s) {
int ans=0;
sort(s.begin(),s.end());
int n= s.size();
if(s[0]!=bottom){
ans=max(ans,s[0]-bottom);
}
if(s[n-1]!=top){
ans=max(ans,top-s[n-1]);
}
for(int i =1;i<n;i++){
ans=max(ans,s[i]-s[i-1]-1);
}
return ans;
}
};T3:按位与结果大于零的最长组合
对数组 nums 执行 按位与 相当于对数组 nums 中的所有整数执行 按位与 。
例如,对 nums = [1, 5, 3] 来说,按位与等于 1 & 5 & 3 = 1 。
同样,对 nums = [7] 而言,按位与等于 7 。
给你一个正整数数组 candidates 。计算 candidates 中的数字每种组合下 按位与 的结果。 candidates 中的每个数字在每种组合中只能使用 一次 。
返回按位与结果大于 0 的 最长 组合的长度。
输入:candidates = [16,17,71,62,12,24,14]
输出:4
解释:组合 [16,17,62,24] 的按位与结果是 16 & 17 & 62 & 24 = 16 > 0 。
组合长度是 4 。
可以证明不存在按位与结果大于 0 且长度大于 4 的组合。
注意,符合长度最大的组合可能不止一种。
例如,组合 [62,12,24,14] 的按位与结果是 62 & 12 & 24 & 14 = 8 > 0 。在开始的时候,我觉得这个是个很难的东西唉。。然后就放弃了,骚骚子一语点醒。
只要把第一组样例的二进制写出来就看出来了
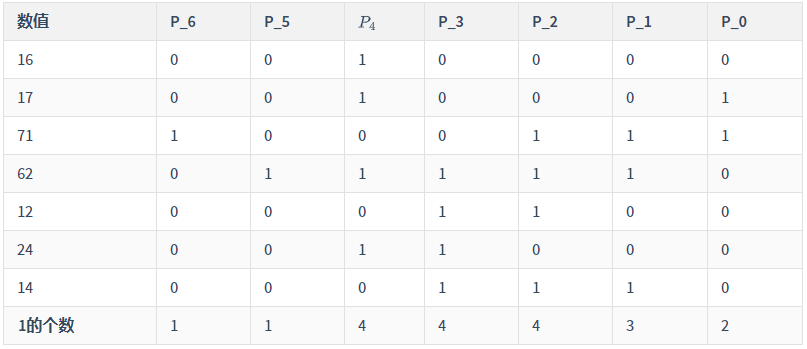
因为要保证与后不为0,也就是说至少要保证有一位不为0。
与的过程中,只要有一位是0,就会出现这一位是0
所以就可以考虑一下每一位的1的个数的最大值,
因此模拟计算一下每个数的1的最大值,然后返回最大值就是答案
class Solution {
public:
int largestCombination(vector<int>& nums) {
int n = nums.size();
vector<int> count(32,0);
for(int i =0;i<32;i++){
for(auto & num:nums){
count[i]+=(num>>i)&1;
}
}
return *max_element(count.begin(),count.end());
}
};T4:统计区间中的整数数目
给你区间的 空 集,请你设计并实现满足要求的数据结构:
- 新增:添加一个区间到这个区间集合中。
- 统计:计算出现在 至少一个 区间中的整数个数。
实现 CountIntervals 类:
CountIntervals()使用区间的空集初始化对象void add(int left, int right)添加区间[left, right]到区间集合之中。int count()返回出现在 至少一个 区间中的整数个数。
注意:区间 [left, right] 表示满足 left <= x <= right 的所有整数 x 。
输入
["CountIntervals", "add", "add", "count", "add", "count"]
[[], [2, 3], [7, 10], [], [5, 8], []]
输出
[null, null, null, 6, null, 8]
解释
CountIntervals countIntervals = new CountIntervals(); // 用一个区间空集初始化对象
countIntervals.add(2, 3); // 将 [2, 3] 添加到区间集合中
countIntervals.add(7, 10); // 将 [7, 10] 添加到区间集合中
countIntervals.count(); // 返回 6
// 整数 2 和 3 出现在区间 [2, 3] 中
// 整数 7、8、9、10 出现在区间 [7, 10] 中
countIntervals.add(5, 8); // 将 [5, 8] 添加到区间集合中
countIntervals.count(); // 返回 8
// 整数 2 和 3 出现在区间 [2, 3] 中
// 整数 5 和 6 出现在区间 [5, 8] 中
// 整数 7 和 8 出现在区间 [5, 8] 和区间 [7, 10] 中
// 整数 9 和 10 出现在区间 [7, 10] 中很明显的合并区间的题,但是交了一发裸的合并区间,TLE了3个用例
然后交了个二分合并区间的板子,直接过
class CountIntervals {
public:
using pii = pair<int, int>;
set <pii> s;
uint64_t count1 = 0;
CountIntervals() {
}
void add(int left, int right) {
pii x = {left, right + 1};
uint64_t before = count1;
int addright = x.second, addleft = x.first;
for (auto p = s.lower_bound({x.first, INT_MIN}); p != s.end() && p->second <= x.second;) {
addright = max(addright, p->first);
addleft = min(addleft, p->second);
count1 -= p->first - p->second;
p = s.erase(p);
}
count1 += addright - addleft;
s.insert({addright, addleft});
}
int count() {
return count1;
}
};
/**
* Your CountIntervals object will be instantiated and called as such:
* CountIntervals* obj = new CountIntervals();
* obj->add(left,right);
* int param_2 = obj->count();
*/









Comments | NOTHING