T1:找到一个数字的 K 美丽值

一个整数 num 的 k 美丽值定义为 num 中符合以下条件的 子字符串 数目：

子字符串长度为 k 。
子字符串能整除 num 。

给你整数 num 和 k ，请你返回 num 的 k 美丽值。

注意：

允许有 前缀 0 。
0 不能整除任何值。

一个 子字符串 是一个字符串里的连续一段字符序列。

输入：num = 240, k = 2
输出：2
解释：以下是 num 里长度为 k 的子字符串：
- "240" 中的 "24" ：24 能整除 240 。
- "240" 中的 "40" ：40 能整除 240 。
所以，k 美丽值为 2 。    

很简单呢，可以先把数字搞成字符串。

然后长度为k的子串就有num.length-k个，分别判断一下能不能整除就行。

很简单的模拟题

class Solution {
public:
    int divisorSubstrings(int num, int k) {
        int ans=0;
        string s= to_string (num);
        for(int i=0;i<s.size()-k+1;i++){
            string t= s.substr(i,k);
            int m= stoi(t);
            if(m==0){
                continue;
            }
            if(num%m==0){
                ans++;
            }
        }
        return ans;
    }
};

T2: 分割数组的方案数

给你一个下标从 0 开始长度为 n 的整数数组 nums 。
如果以下描述为真，那么 nums 在下标 i 处有一个 合法的分割 ：

前 i + 1 个元素的和 大于等于 剩下的 n - i - 1 个元素的和。
下标 i 的右边 至少有一个 元素，也就是说下标 i 满足 0 <= i < n - 1 。

请你返回 nums 中的 合法分割 方案数。

输入：nums = [10,4,-8,7]
输出：2
解释：
总共有 3 种不同的方案可以将 nums 分割成两个非空的部分：
- 在下标 0 处分割 nums 。那么第一部分为 [10] ，和为 10 。第二部分为 [4,-8,7] ，和为 3 。因为 10 >= 3 ，所以 i = 0 是一个合法的分割。
- 在下标 1 处分割 nums 。那么第一部分为 [10,4] ，和为 14 。第二部分为 [-8,7] ，和为 -1 。因为 14 >= -1 ，所以 i = 1 是一个合法的分割。
- 在下标 2 处分割 nums 。那么第一部分为 [10,4,-8] ，和为 6 。第二部分为 [7] ，和为 7 。因为 6 < 7 ，所以 i = 2 不是一个合法的分割。
所以 nums 中总共合法分割方案受为 2 。

很裸的一个前缀和的题吧，先计算前缀和，在扫描过程中就可以分别得到前后的值，判断大小即可

但是这道，因为

• 2 <= nums.length <= 105

• -105 <= nums[i] <= 105

  没有注意看数据范围最大1e10,前缀和没有开longlong溢出错了一发

​

class Solution {
public:
    int waysToSplitArray(vector<int>& nums) {
        vector<long long > num(nums.begin(),nums.end());
        for(int i =1;i<num.size();i++){
            num[i]+=num[i-1];
        }
        int ans=0;
        for(int i =0;i<num.size()-1;i++){
            if(num[num.size()-1]-num[i]<=num[i]){
                ans++;
            }
        }
        return ans;
    }
};

T3：毯子覆盖的最多白色砖块数

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。

同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子。

请你返回使用这块毯子，最多 可以盖住多少块瓷砖。

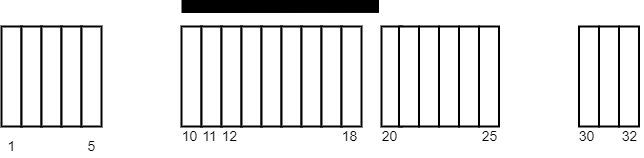
输入：tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出：9
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖，所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出，瓷砖无法覆盖超过 9 块瓷砖。

这道题其实很容易证明，最大的一定是从某一块儿的左边开始的，然后最远到哪儿去找一下就行

那这样的话，就是从左往右的左端点开始扫描，最远到哪儿，到了以后覆盖了多少块儿

一开始直接双指针往后TLE了

然后就换了二分，就过了，注意用前缀和优化

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>> &m, int carpetLen) {
        sort(m.begin(), m.end());
        vector<int> sum(m.size() + 1, 0);
        vector<int> l(m.size(), 0);
        sum[1] = m[0][1] - m[0][0] + 1;
        l[0] = m[0][0];
        for (int i = 1; i < m.size(); i++) {
            sum[i + 1] = sum[i] + m[i][1] - m[i][0] + 1;
            l[i] = m[i][0];
        }
        int n = m.size();
        int ans = 0;
        int i, j;
        int lastj = 0;
        for (i = 0; i < n; i++) {
            int j = lower_bound(l.begin() + lastj, l.end(), m[i][0] + carpetLen) - l.begin() - 1;
            lastj = j;
            int cnt = sum[j] - sum[i]+ min(m[i][0] + carpetLen - 1, m[j][1]) - m[j][0] + 1;
            ans = max(ans, cnt);
        }
        return ans;
    }
};

T4:最大波动的子字符串

字符串的 波动 定义为子字符串中出现次数 最多 的字符次数与出现次数 最少 的字符次数之差。

给你一个字符串 s ，它只包含小写英文字母。请你返回 s 里所有 子字符串的 最大波动 值。

子字符串 是一个字符串的一段连续字符序列。

输入：s = "aababbb"
输出：3
解释：
所有可能的波动值和它们对应的子字符串如以下所示：
- 波动值为 0 的子字符串："a" ，"aa" ，"ab" ，"abab" ，"aababb" ，"ba" ，"b" ，"bb" 和 "bbb" 。
- 波动值为 1 的子字符串："aab" ，"aba" ，"abb" ，"aabab" ，"ababb" ，"aababbb" 和 "bab" 。
- 波动值为 2 的子字符串："aaba" ，"ababbb" ，"abbb" 和 "babb" 。
- 波动值为 3 的子字符串 "babbb" 。
所以，最大可能波动值为 3 。

有点质量的一道题，当场没出，补

1.出现次数最多与最少的字母,必定是a-z中的一对不同字母的组合,记出现次数最多的为x,出现次数少的为b

    2.枚举x与y的二维组合,记字符串中的x=1,y=1,然后其余的字母为0,那么其出现次数的差转化为子数组的和
        参考:最大子数组的和就可以用动态规划进行处理!
    3.有一点主要注意的是,x与y在子串中均需要出现(其实是保证y要出现),因此其转移方程就有不同
        记:dp[i][0]为以s[i-1]结尾的子串和的最大值
            dp[i][1]为以s[i-1]结尾的(且包含y)子串和的最大值
            记s[i-1]对应的数字为v,即s[i]=x,v=1;s[i]=y,v=-1;s[i]=其他,v=0
        3.1 显然:dp[i][0]=max(dp[i-1][0]+v,v)
        3.2 而dp[i-1]的转移就需要看s[i-1]是否为y决定的
            3.2.1 当s[i-1]==y时,有两种转移途径,要么自成一体,要么拉上前面的dp[i-1][0],两者取最大值
            (这种情况前面有没有y都行,必定是没有y的会更大,因此可以直接舍弃dp[i-1][1])
                即dp[i][1]=max(dp[i-1][0]+v,v)
            3.2.2 当s[i-1]!=y时,就只能从前面有y的继承过来,dp[i][1]=dp[i-1][1]+v
        遍历过程中维护最大的dp[i][1]就是组合x与y的最大波动值max
    4.最后维护好每种组合对应的max就是答案

class Solution {
public:
    int largestVariance(string s) {
        int n = s.size();
        int ret = 0;
        for (char a = 'a'; a <= 'z'; ++a) {
            for (char b = 'a'; b <= 'z'; ++b) {
                // j: 当前子串的起始下标
                // k: 上一次出现b的下标
                for (int i = 0, j = -1, k = -1, cnt = 0; i < n; ++i) {
                    if (a == b) {
                        continue;
                    }
                    if (s[i] == a) {
                        cnt++;
                    } else if (s[i] == b) {
                        cnt--;
                        k = i;
                    }
                    if (k != -1) {
                        if (j < k) {
                            ret = max(ret, cnt);
                        } else {
                            ret = max(ret, cnt - 1);
                        }
                        if (cnt < 0) {
                            cnt = 0;
                            j = i;
                        }
                    }
                }
            }
        }
        return ret;
    }
};