Count Asterisks3

You are given a string s, where every two consecutive vertical bars '|' are grouped into a pair. In other words, the 1st and 2nd '|' make a pair, the 3rd and 4th '|' make a pair, and so forth.

Return the number of '*' in s, excluding the '*' between each pair of '|'.

Note that each '|' will belong to exactly one pair.

Example 1:

Input: s = "l|*e*et|c**o|*de|"
Output: 2
Explanation: The considered characters are underlined: "l|*e*et|c**o|*de|".
The characters between the first and second '|' are excluded from the answer.
Also, the characters between the third and fourth '|' are excluded from the answer.
There are 2 asterisks considered. Therefore, we return 2.

两个竖线之间算一组，找奇数组之间的*的和，模拟一下，用py切片

class Solution:
    def countAsterisks(self, s: str) -> int:
        ls=s.split('|')[::2]
        ans=0
        for i in ls:
            ans+=i.count('*')
        return ans

Count Unreachable Pairs of Nodes in an Undirected Graph

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

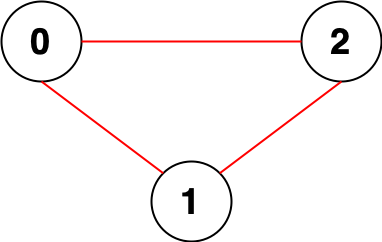
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

到达不了的对儿数，并查集搞一下连通分量，然后计数就行

class Solution {
public:
    int f[100001];
    int find(int x){
        if(f[x]==x){
            return x;
        }
        return f[x]=find(f[x]);
    }
    long long countPairs(int n, vector<vector<int>>& edges) {
        for(int i = 0;i<n;i++){
            f[i]=i;
        }
        for(auto & e:edges){
            f[find(e[0])]=find(e[1]);
        }
        map<long long , long long> m;
        for(int i =0;i<n;i++){
            m[find(i)]++;
        }
        long long ans=0;
        for(auto&[x,y]:m){
            ans+=(n-y)*y;
        }
        return ans/2;
    }
};

Maximum XOR After Operations

You are given a 0-indexed integer array nums. In one operation, select any non-negative integer x and an index i, then update nums[i] to be equal to nums[i] AND (nums[i] XOR x).

Note that AND is the bitwise AND operation and XOR is the bitwise XOR operation.

Return the maximum possible bitwise XOR of all elements of nums after applying the operation any number of times.

Example 1:

Input: nums = [3,2,4,6]
Output: 7
Explanation: Apply the operation with x = 4 and i = 3, num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
Now, nums = [3, 2, 4, 2] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
It can be shown that 7 is the maximum possible bitwise XOR.
Note that other operations may be used to achieve a bitwise XOR of 7.

重复了吧和前几周，就是看看一下1的个数。异或的话，控制一下奇数的个数就行。与运算

class Solution {
public:
    int maximumXOR(vector<int>& nums) {
        int ans=nums[0];
        for(int i = 1;i<nums.size();i++){
            ans|=nums[i];
        }
        return ans;
    }
};

Number of Distinct Roll Sequences

You are given an integer n. You roll a fair 6-sided dice n times. Determine the total number of distinct sequences of rolls possible such that the following conditions are satisfied:

1. The greatest common divisor of any adjacent values in the sequence is equal to 1.
2. There is at least a gap of 2 rolls between equal valued rolls. More formally, if the value of the ith roll is equal to the value of the jth roll, then abs(i - j) > 2.

Return the total number of distinct sequences possible. Since the answer may be very large, return it modulo 109 + 7.

Two sequences are considered distinct if at least one element is different.

Example 1:

Input: n = 4
Output: 184
Explanation: Some of the possible sequences are (1, 2, 3, 4), (6, 1, 2, 3), (1, 2, 3, 1), etc.
Some invalid sequences are (1, 2, 1, 3), (1, 2, 3, 6).
(1, 2, 1, 3) is invalid since the first and third roll have an equal value and abs(1 - 3) = 2 (i and j are 1-indexed).
(1, 2, 3, 6) is invalid since the greatest common divisor of 3 and 6 = 3.
There are a total of 184 distinct sequences possible, so we return 184.

DP吧，DFS可能要tle，三维dp，记录当前数和上一个。试一下，啊我是个傻逼！

class Solution {
public:
    int p=1000000007;
    int f[10001][7][7];
    int e[7][7];
    int distinctSequences(int n) {
        if(n==1){
            return 6;
        }
        vector<vector<int>> q(7);
        for(int i = 1;i<7;i++){
            for(int j = 1;j<7;j++){
                e[i][j]=__gcd(i,j);
                f[0][i][j]=0;
                if(__gcd(i,j)==1&&i!=j){
                    q[i].push_back(j);
                }
                if(i==j||__gcd(i,j)!=1){
                    f[1][i][j]=0;
                }else{
                    f[1][i][j]=1;
                }
            }
        }
        for(int i =2;i<n;i++){
            for(int a=1;a<=6;a++){
                for(auto& b:q[a]){
                    f[i][a][b]=0;
                    for(int c=1;c<=6;c++){
                        if(__gcd(a,b)!=1||__gcd(b,c)!=1||a==c){
                            continue;
                        }
                        f[i][a][b]=(f[i][a][b]+f[i-1][b][c])%p;
                    }
                }
            }
        }
        long long ans=0;
        for(int i = 1; i<=6;i++){
            for(int j =1;j<=6;j++){
                ans+=f[n-1][i][j];
                ans=ans%p;
            }
        }
        return ans;      
    }
};