周日要考试辣，一直复习也迷糊，不如花一个小时上个DIV4换换脑子哦。

不对我期末不考英语也不考数据结构与算法，我搞这玩意干啥？

A. YES or YES?

There is a string s of length 3, consisting of uppercase and lowercase English letters. Check if it is equal to "YES" (without quotes), where each letter can be in any case. For example, "yES", "Yes", "yes" are all allowable.

给个字符串，判断是不是yes的变形，全换成大写。python用户是不是乐呢？

#include <bits/stdc++.h>

using namespace std;

void solve() {
    string s;
    cin >> s;
    for (auto &ch: s) {
        ch = toupper(ch);
    }
    if (s == "YES") {
        cout << "YES" << endl;
    } else {
        cout << "NO" << endl;
    }

}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

B. ICPC Balloons

In an ICPC contest, balloons are distributed as follows:

• Whenever a team solves a problem, that team gets a balloon.

• The first team to solve a problem gets an additional balloon.

  A contest has 26 problems, labelled A, B, C, ..., Z. You are given the order of solved problems in the contest, denoted as a string s, where the i-th character indicates that the problem si has been solved by some team. No team will solve the same problem twice.

Determine the total number of balloons that the teams recieved. Note that some problems may be solved by none of the teams.

ICPC的规则嘛。发气球，第一个过的发俩，否则发一个，就看看发俩的有几次，用set记录不重复的字符个数。两个求和

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    string s;
    cin >> s;
    set<char> m;
    long long ans = 0;
    for (auto &ch: s) {
        m.insert(ch);
    }
    cout << m.size() + s.size() << endl;

}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

C. Cypher

Luca has a cypher made up of a sequence of n wheels, each with a digit ai written on it. On the i-th wheel, he made b_i

moves. Each move is one of two types:

up move (denoted by U): it increases the i-th digit by 1. After applying the up move on 9, it becomes 0.

down move (denoted by D): it decreases the i-th digit by 1. After applying the down move on 0, it becomes 9.

Luca knows the final sequence of wheels and the moves for each wheel. Help him find the original sequence and crack the cypher.

给操作了，给最终了，还原，取模，但是为了避免减小导致的负数，模前+10

if'U':m[i]=（m[i]+9）%10

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> m(n);
    for (int i = 0; i < n; i++) {
        cin >> m[i];
    }
    for (int i = 0; i < n; i++) {
        int tmp;
        cin >> tmp;
        string f;
        cin >> f;
        for (auto &ch: f) {
            if (ch == 'U') {
                m[i] = (m[i] + 9) % 10;
            } else {
                m[i] = (m[i] + 11) % 10;
            }
        }
    }
    for (auto &t: m) {
        cout << t << " ";
    }
    cout << "\n";

}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

D. Double Strings

You are given n strings s1,s2,…,sn of length at most 8*.

For each string si, determine if there exist two strings sj and sk such that si=sj+sk. That is, si is the concatenation of sj and sk. Note that jcan be equal to k.

Recall that the concatenation of strings s and t is s+t=s1s2…spt1t2…tq, where p and q are the lengths of strings s and t respectively. For example, concatenation of "code" and "forces" is "codeforces".

给一组字符串，看某一个串是不是可以由另外两个串链接组成

由于长度最大8，每个串就可以拆成n中情况。很快就哈希模拟了。

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<string> m(n);
    map<string, bool> c;
    for (int i = 0; i < n; i++) {
        cin >> m[i];
        c[m[i]] = 1;
    }
    long long ans = 0;
    for (int i = 0; i < n; i++) {
        bool f= true;
        for (int l = 1; l < m[i].size()&&f; l++) {
            string a = m[i].substr(0, l);
            string b = m[i].substr(l);
            if (c[a] && c[b]) { cout<<1;f= false; }
        }
        if(f){
            cout<<0;
        }
    }
    cout << endl;
}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

E. Mirror Grid

You are given a square grid with n rows and n columns. Each cell contains either 0 or 1.

In an operation, you can select a cell of the grid and flip it (from 0→1 or 1→0). Find the minimum number of operations you need to obtain a square that remains the same when rotated 0∘, 90∘, 180∘ and 270∘.

The picture below shows an example of all rotations of a grid.

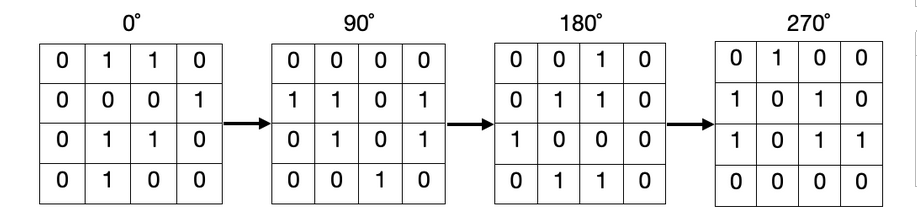
转圈，那就哈扫1/4就行了。然后看这个小正方形中的每个格转后的四个坐标01和1谁多，谁少就给结果加上谁

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<string> m(n);
    for (int i = 0; i < n; i++) {
        cin >> m[i];
    }
    map<pair<int, int>, bool> f;
    long long ans = 0;

    for (int i = 0; i < (n + 2) / 2; i++) {
        for (int j = 0; j < (n + 2) / 2; j++) {
            if (f[{i, j}]) {
                continue;
            }
            f[{n - j - 1, i}] = 1;
            f[{n - i - 1, n - j - 1}] = 1;
            f[{j, n - i - 1}] = 1;
            f[{i, j}] = 1;
            int count[2] = {0, 0};
            count[m[n - j - 1][i] - '0']++;
            count[m[n - i - 1][n - j - 1] - '0']++;
            count[m[j][n - i - 1] - '0']++;
            count[m[i][j] - '0']++;
            ans += min(count[0], count[1]);
        }
    }
    cout << ans << endl;
}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

F. Yet Another Problem About Pairs Satisfying an Inequality

You are given an array a1,a2,…an. Count the number of pairs of indices 1≤i,j≤n such that ai<i<aj<j.

一句话就看出来了，不会有人看不出来这是前缀和吧，但是我瞎！没看到ll的结果wa了

#include <bits/stdc++.h>

using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<pair<int, int>> m;
    int mx = 0;
    for (int i = 0; i < n; i++) {
        int tmp;
        cin >> tmp;
        if (tmp < i + 1) {
            m.push_back({tmp, i + 1});
            mx = max(mx, i + 1);
        }
    }
    map<int, int> c;
    for (auto &[x, y]: m) {
        c[x]++;
    }
    vector<int> pre(1, 0);
    for (int i = 1; i <= mx; i++) {
        pre.push_back(pre.back() + c[i]);
    }
    long long ans = 0;
    for (auto &[x, y]: m) {
        ans += pre.back() - pre[y];
    }
    cout << ans << endl;

}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}

G. Good Key, Bad Key

There are n chests. The i-th chest contains ai coins. You need to open all n chests in order from chest 1 to chest n.

There are two types of keys you can use to open a chest:

• a good key, which costs k coins to use;
• a bad key, which does not cost any coins, but will halve all the coins in each unopened chest, including the chest it is about to open. The halving operation will round down to the nearest integer for each chest halved. In other words using a bad key to open chest i will do ai=⌊ai2⌋, ai+1=⌊ai+12⌋,…,an=⌊an2⌋
• any key (both good and bad) breaks after a usage, that is, it is a one-time use.

You need to use in total n keys, one for each chest. Initially, you have no coins and no keys. If you want to use a good key, then you need to buy it.

During the process, you are allowed to go into debt; for example, if you have 1 coin, you are allowed to buy a good key worth k=3 coins, and your balance will become −2 coins.

Find the maximum number of coins you can have after opening all n chests in order from chest 1 to chest n.

可用好的，好的就有成本，可以用坏的，坏的就剩下的都减半。

因为如果先用好的后用坏的，得到的是$x+\frac{y}{2}$

先用坏的后用好的，得到的是$\frac{x+y}{2}$

所以你就会知道，用了一个坏的以后，全用坏的。

因此就可以线性的模拟一下每个点用坏的后的费用取max

并且这中间只需要模拟31个，因为最大1e9，小于2^32

#include <bits/stdc++.h>

using namespace std;

void solve() {
    long long n, k;
    cin >> n >> k;
    vector<long long> m(n);
    long long sum = 0;
    for (int i = 0; i < n; i++) {
        cin >> m[i];
        sum += m[i];
    }
    long long ans = sum - n * k;
    long long now = 0;
    for (int i = 0; i < n; i++) {
        long long cnt = now - i * k;
        long long p = 2;
        for (int j = i; j < i + 32 && j < n; j++) {
            cnt += m[j] / p;
            p *= 2ll;

        }
        if (cnt > ans) {
            ans = cnt;
        }
        now += m[i];
    }
    cout << ans << endl;
}

signed main() {
    int T = 1;
    cin >> T;
    while (T--) {
        solve();
    }
}