公钥密码体制

•私钥密码体制存在秘钥量大：$n$个用户之间互相通信一共需要$C_n^2=\frac{n(n-1)}{2}$个 密钥。

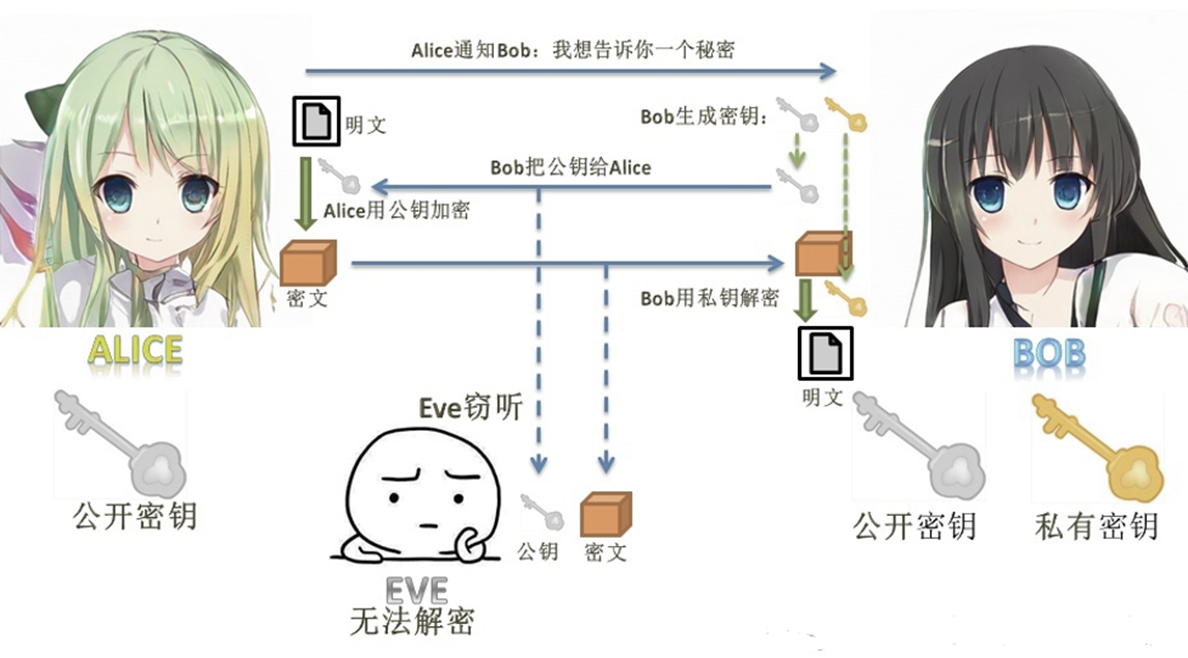
•公钥密码体制加密密钥$P_k$公开，但解密密钥$S_k$ 是保密的。

来看一道崭新的算法题（年龄小于24小时）

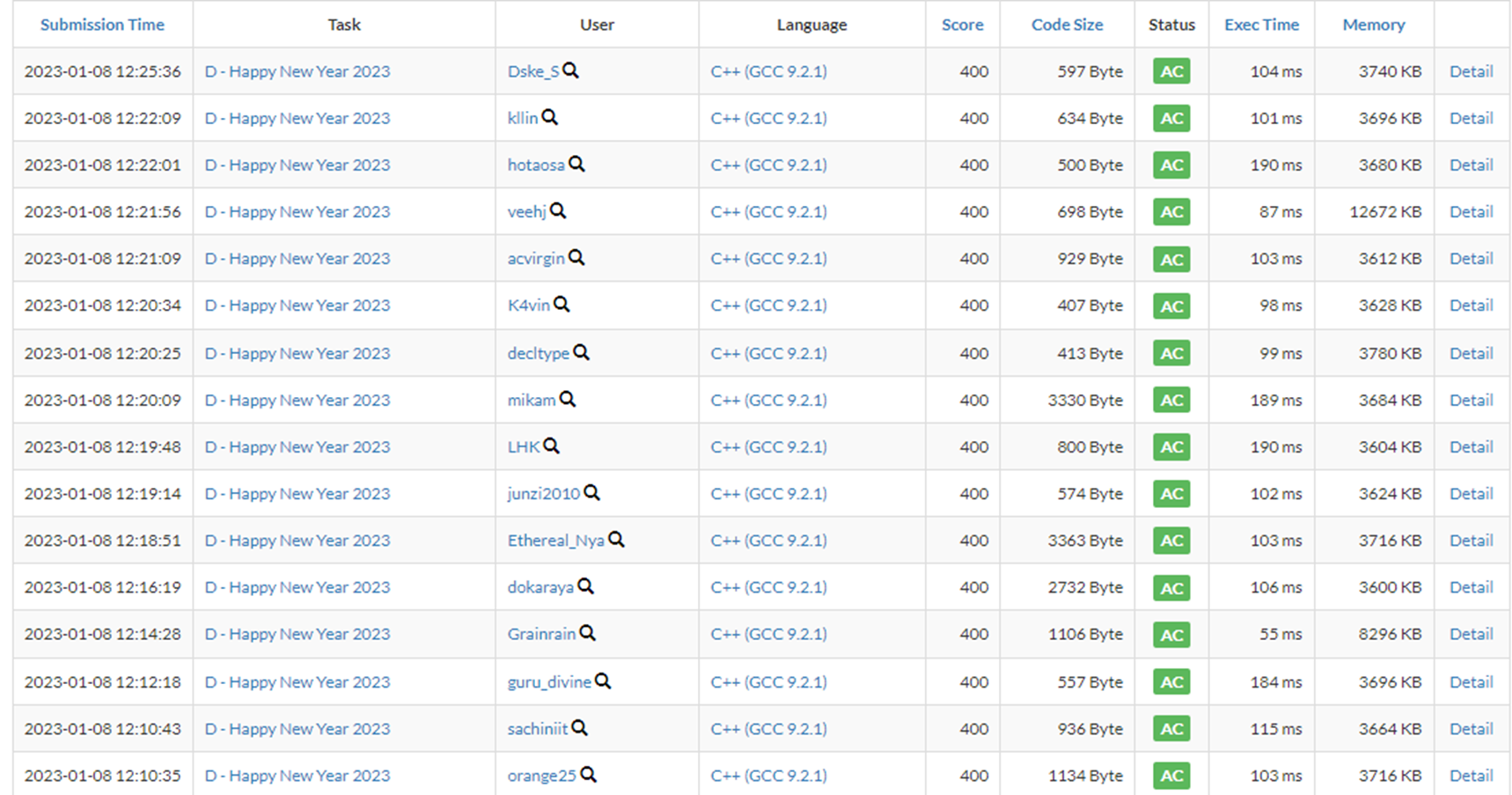
对于两个素数$p$和$q$，可以瞬间完成$n=p*q$的运算。

但是如果想从$n$分解出$p$和$q$，则需要进行因式分解

常见的因子分解的方法有$O(\sqrt{n})$的枚举因子方法，

还有预处理素数后优化到最差$O(\frac{n}{3})$的方法

也有不保证$100\%$准确的Pallord算法$O(\sqrt[4]{n})$

举个通俗的例子，如果对于一个程序来说，输入规模 $n=10^9$的话：

$O(1)$的算法大约只用1次运算，普通电脑$ 10^{-9}$ 秒就能算完。

$O(logn)$大约会用30次计算（log的底数是2），普通电脑 $10^{-8}$秒算完。

$O(n)$大约就是 $10^9$次计算，普通电脑需要一秒左右。

$O(n^2) $大约是$ 10^{18}$次计算，普通电脑大概要30年。

$O(n!)$的话，人类所有电脑加在一起，等太阳炸了都算不完。

但是如果二进制下的n大于2048位

计算机是目前来说是基本无解的QwQ

因此就可以基于这个性质来设计密码

RSA加密原理

如何利用这个特点呢？！！！

请注意！现在神奇的事情发生了！对于一个与n互质的数a：

因为 $a^{φ(n)} ≡1 (mod n)$

所以 $a^{kφ(n)} ≡1 (mod n)$

所以 $a^{(kφ(n)+1)}≡a (mod n)$

不妨吧$kφ(n)+1$拆成两个数$e$和$d$的乘积，则可以表示为，此时有$ed=kφ(n)+1$

所以 $a^{ed}≡a (mod n)$

所以，若$ c≡a^e (mod n)$, 则$c^d≡a^{ed}≡a（mod n）$

（1）选定两个超大素数p和q。

在此需要用到大素数生成方法，方法较多。

以素数分布平均间距可逼近为$π(x)=\frac{x}{(t(x))}=\frac{x}{(ln⁡(x)-1)}$的结论来考虑，可以先生成一个随机大数，然后从其开始可以遍历连续的一部分奇数，复杂度并不大，最差的搜索长度就是$π(x)$ 。

然后通过快速判定某个数是不是素数来决定搜索的跳出

（1b）$Fermat $素性测试

我们可以根据 费马小定理 得出一种检验素数的思路：

基本思想是不断地选取在$[2,n-1]$中的基$a$，并检验是否每次都有$a^{n-1}≡1(mod n) $

那么经过$t$轮测试,$p$不是素数的概率为$\frac{1}{4^t}$

我习惯用$2,3,5,7,11,13,17,19$这几个数进行判断

在信息学范围内出错率为$0\%$(不带高精)

（2）计算$n=p∗q,ϕ(n)=(p-1)(q-1)$

我们假设上一步选定的$p=11$和$q=13$,则$n=143$

根据欧拉函数的定义，可以知道素数m的因数只有$1$和$m$，所以小于等于$m$的数，除了$m$都和他互质

即$ϕ(p)=(p-1)$ 其中$p$为素数。

根据此可知，$n=pq$中，质因子除了有$1q,2q,3q…(p-1),pq$和$1p,2p,3p…(q-1)p,pq$共有$p+q-1$个，

因此n以内和n互质的数有$pq-(p+q-1)=pq-p-q+1=(p-1)(q-1)$个

则$ϕ(n)=120$

（4）此时密钥生成完毕

根据$ a^{ed}≡a (mod n)$

$ c≡a^{e} (mod n)$

$ c^d≡a^{ed}≡a(mod n)$

可知加密方需要$e$和$n$两个数据，解密方需要$d$和$n$两个数据

由此公钥即为${e,n}$，私钥为${d,n}$