给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号:
- 最高有效位 上的数字分配到 正 号。
- 剩余每位上数字的符号都与其相邻数字相反。
返回所有数字及其对应符号的和。
示例 1:
输入:n = 521
输出:4
解释:(+5) + (-2) + (+1) = 4示例 2:
输入:n = 111
输出:1
解释:(+1) + (-1) + (+1) = 1示例 3:
输入:n = 886996
输出:0
解释:(+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0提示:
- $1 <= n <= 10^9$
模拟吧
class Solution {
public:
int alternateDigitSum(int n) {
vector<int> a;
while (n) {
a.push_back(n % 10);
n /= 10;
}
int ans = 0;
bool s = 1;
// std::reverse(a.begin(), a.end());
while (a.size()) {
if (s) ans += a.back();
else ans -= a.back();
s = !s;
a.pop_back();
}
return ans;
}
};班里有 m 位学生,共计划组织 n 场考试。给你一个下标从 0 开始、大小为 m x n 的整数矩阵 score ,其中每一行对应一位学生,而 score[i][j] 表示第 i 位学生在第 j 场考试取得的分数。矩阵 score 包含的整数 互不相同 。
另给你一个整数 k 。请你按第 k 场考试分数从高到低完成对这些学生(矩阵中的行)的排序。
返回排序后的矩阵。
示例 1:
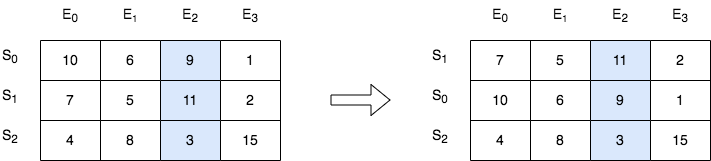
输入:score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
输出:[[7,5,11,2],[10,6,9,1],[4,8,3,15]]
解释:在上图中,S 表示学生,E 表示考试。
- 下标为 1 的学生在第 2 场考试取得的分数为 11 ,这是考试的最高分,所以 TA 需要排在第一。
- 下标为 0 的学生在第 2 场考试取得的分数为 9 ,这是考试的第二高分,所以 TA 需要排在第二。
- 下标为 2 的学生在第 2 场考试取得的分数为 3 ,这是考试的最低分,所以 TA 需要排在第三。示例 2:
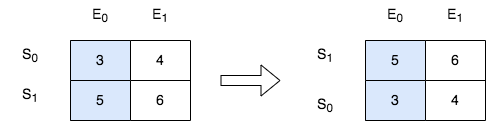
输入:score = [[3,4],[5,6]], k = 0
输出:[[5,6],[3,4]]
解释:在上图中,S 表示学生,E 表示考试。
- 下标为 1 的学生在第 0 场考试取得的分数为 5 ,这是考试的最高分,所以 TA 需要排在第一。
- 下标为 0 的学生在第 0 场考试取得的分数为 3 ,这是考试的最低分,所以 TA 需要排在第二。提示:
m == score.lengthn == score[i].length1 <= m, n <= 2501 <= score[i][j] <= 1e5score由 不同 的整数组成0 <= k < n
按照关键字排序,一行
class Solution {
public:
vector <vector<int>> sortTheStudents(vector <vector<int>> &s, int k) {
sort(s.begin(), s.end(), [&](auto &a, auto &b) { return a[k] > b[k]; });
return s;
}
};给你两个下标从 0 开始的 二元 字符串 s 和 target ,两个字符串的长度均为 n 。你可以对 s 执行下述操作 任意 次:
- 选择两个 不同 的下标
i和j,其中0 <= i, j < n。 - 同时,将
s[i]替换为 (s[i]ORs[j]) ,s[j]替换为 (s[i]XORs[j]) 。
例如,如果 s = "0110" ,你可以选择 i = 0 和 j = 2,然后同时将 s[0] 替换为 (s[0] OR s[2] = 0 OR 1 = 1),并将 s[2] 替换为 (s[0] XOR s[2] = 0 XOR 1 = 1),最终得到 s = "1110" 。
如果可以使 s 等于 target ,返回 true ,否则,返回 false 。
示例 1:
输入:s = "1010", target = "0110"
输出:true
解释:可以执行下述操作:
- 选择 i = 2 和 j = 0 ,得到 s = "0010".
- 选择 i = 2 和 j = 1 ,得到 s = "0110".
可以使 s 等于 target ,返回 true 。示例 2:
输入:s = "11", target = "00"
输出:false
解释:执行任意次操作都无法使 s 等于 target 。11可以通过xor出现0,通过or出现1
10可以通过or出现1,通过xor也是1
00只能出现0
也就是一边没有1的时候,另一边也不能有1,一边没有0的时候另一边也不能没有0
class Solution {
public:
bool makeStringsEqual(string s, string t) {
bool f1 = find(s.begin(), s.end(), '1') != s.end();
bool f2 = find(t.begin(), t.end(), '1') != t.end();
return f1 == f2;
}
};给你一个整数数组 nums 和一个整数 k 。
将数组拆分成一些非空子数组。拆分的 代价 是每个子数组中的 重要性 之和。
令 trimmed(subarray) 作为子数组的一个特征,其中所有仅出现一次的数字将会被移除。
- 例如,
trimmed([3,1,2,4,3,4]) = [3,4,3,4]。
子数组的 重要性 定义为 k + trimmed(subarray).length 。
- 例如,如果一个子数组是
[1,2,3,3,3,4,4],trimmed([1,2,3,3,3,4,4]) = [3,3,3,4,4]。这个子数组的重要性就是k + 5。
找出并返回拆分 nums 的所有可行方案中的最小代价。
子数组 是数组的一个连续 非空 元素序列。
示例 1:
输入:nums = [1,2,1,2,1,3,3], k = 2
输出:8
解释:将 nums 拆分成两个子数组:[1,2], [1,2,1,3,3]
[1,2] 的重要性是 2 + (0) = 2 。
[1,2,1,3,3] 的重要性是 2 + (2 + 2) = 6 。
拆分的代价是 2 + 6 = 8 ,可以证明这是所有可行的拆分方案中的最小代价。示例 2:
输入:nums = [1,2,1,2,1], k = 2
输出:6
解释:将 nums 拆分成两个子数组:[1,2], [1,2,1] 。
[1,2] 的重要性是 2 + (0) = 2 。
[1,2,1] 的重要性是 2 + (2) = 4 。
拆分的代价是 2 + 4 = 6 ,可以证明这是所有可行的拆分方案中的最小代价。示例 3:
输入:nums = [1,2,1,2,1], k = 5
输出:10
解释:将 nums 拆分成一个子数组:[1,2,1,2,1].
[1,2,1,2,1] 的重要性是 5 + (3 + 2) = 10 。
拆分的代价是 10 ,可以证明这是所有可行的拆分方案中的最小代价。提示:
1 <= nums.length <= 10000 <= nums[i] < nums.length1 <= k <= 1e9
是个dp,但是好像记忆化更好写,大概思路就是记忆化搜索一下每个尾巴的情况下的最小价值需要搞一搞,语法都不会了擦
class Solution {
public:
int minCost(vector<int> &nums, int k) {
int n = nums.size();
int re[1001] = {-1};
memset(re, -1, sizeof re);
std::function<int(int)> dfs = [&](int x) {
if (re[x] != -1) return re[x];
if (x >= n) return 0;
int ans = INT_MAX, cnt = 0;
int count[1001] = {0};
for (int i = x; i < n; i++) {
if (count[nums[i]] == 1) cnt += 2;
else if (count[nums[i]] > 1) cnt++;
count[nums[i]]++;
ans = min(ans, dfs(i + 1) + cnt + k);
}
return re[x] = ans;
};
return dfs(0);
}
};








Comments | NOTHING